Non-equilibrium quantum dynamics |
|
 |
Predicting the time evolution of quantum systems after initialized in a non-equilibrium state has posed a major challenge to researchers since the birth of quantum mechanics. In general, exact methods are only present for small or non-interacting systems. However, exact or very efficient methods (e.g., bosonization, Bethe-ansatz techniques, matrix product state algorithms) have been developed in the past decades which methods can be applied in one-dimensional systems. These methods enable for the study of fundamental phenomena like non-equilibrium transport, thermalization, or the development of non-equilibrium steady states in these systems.
Figure reference: M. Kormos , M. Collura, G. Takács, and P. Calabrese, Nature Physics 13, 246–249(2017). |
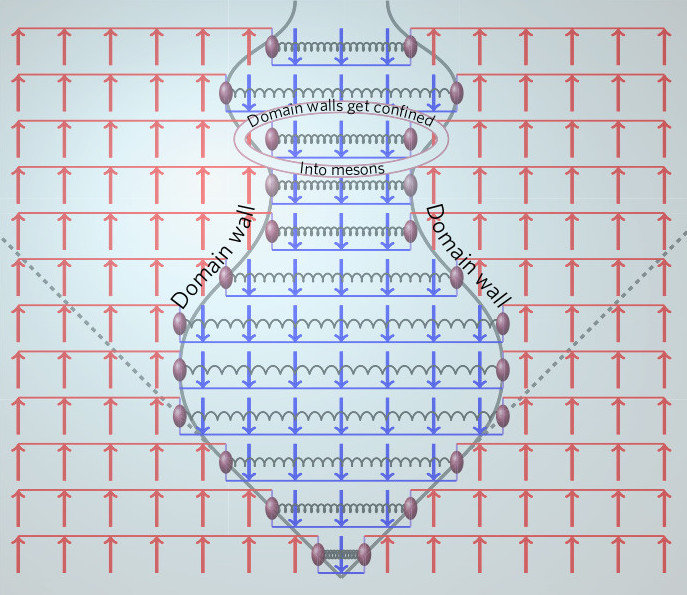
Strongly correlated quantum systems |
|
 |
The structure of many-body quantum states that appear in strongly interacting quantum systems is of great interest to researchers. The strong interactions lead to strong quantum correlations between the constituents of these systems. Good examples for such states are the Luttinger liquids in one dimension or the Wigner crystal state of electrons with strong Coulomb repulsion. State of the art experimental techniques with cold atoms or nano-sized devices allow for detailed experimental investigation of these systems, and the rapid development of the experiments motivates also the theoretical research. Strongly correlated states are usually hard to describe because these states usually cannot be reached by perturbation theory around the non-interacting limit.
Figure reference: I. Shapir, A. Hamo, S. Pecker, C. P. Moca, Ö. Legeza, G. Zaránd, S. Ilani, Science 364, 870-875 (2019).
|
Tensor network based simulations |
|
 |
Classical simulation of quantum systems with our digital computers can be performed, in general, rather inefficiently due to the exponentially large many-body Hilbert space. However, the physically relevant quantum states (for example, low energy states of systems with local interactions) can be treated more efficiently if one exploits the fact that quantum entanglement is usually weak in these states. The weak entanglement enables for tensor network representation of these states. Various algorithms have been developed for tensor network states in the last three decades (e.g., DMRG for ground state calculations, TEBD or TDVP for real time simulations) promoting tensor network approach to be one of the most versatile numerical tools for physicists. We have also developed sophisticated algorithms in which we can exploit Abelian and non-Abelian symmetries of the system or simulate open systems that are coupled to an external heat bath.
Figure reference: M. A. Werner, C. P. Moca, Ö. Legeza, G. Zaránd, Phys. Rev. B 102, 155108 (2020).
|

